The Story of Joon
2015 ACM-ICPC 한국 예선 F - 파일 합치기 본문
11066번: 파일 합치기
문제 소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을
www.acmicpc.net
이 문제는 2015년 ACM-ICPC 예선에 나왔던 문제로, DP 테이블을 정의하면 \(O(K^3)\)의 시간복잡도로 어렵지 않게 풀리는 문제다. 난이도는 solved.ac 기준 골드 3에 해당한다.
\(DP[i][j]\) := \(i\)번째 파일부터 \((j - 1)\)번째 파일까지를 합치는 데 드는 최소 비용
\(S[i][j]\) := \(i\)번째 파일부터 \((j - 1)\)번째 파일까지 크기의 총합
\(DP[i][j] = \min_{i<k<j}(DP[i][k] + DP[k][j] + S[i][j])\)
하지만 이 문제는 \(O(K^3)\)보다 빠르게 푸는 방법이 존재한다. 그중 두 가지 방법을 이 포스트에서 소개하고자 한다.
\(O(K^2)\)
13974번: 파일 합치기 2
소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을 합칠
www.acmicpc.net
위와 같은 형태의 DP는, 최적화할 수 있는 방법이 존재한다. 이 문제는 사실 약간 변형하면 Optimal Binary Search Tree 문제의 특수한 경우임을 알 수 있고, optimal binary search tree problem을 해결하는 여러 가지 알고리즘 중 Donald Knuth의 알고리즘이 우리나라에 Knuth Optimization이라는 이름으로 잘 알려져 있다. 위 파일 합치기 2는 다른 조건 변화 없이 \(K\)의 제한이 5000까지 늘어난 문제이고, Knuth algorithm을 사용하도록 의도되었으며, 이 알고리즘이 어느 정도 알려져 있음을 고려해 난이도는 solved.ac 기준 플래티넘 2로 평가되고 있다.
Knuth algorithm은 아래와 같은 observation을 바탕으로 시간복잡도를 \(O(K^2)\)까지 단축되며, 이 observation의 정당성과 이렇게 시간복잡도가 줄어드는 것의 증명은 추가 예정이다.
\(K[i][j]\) := 위 정의에서 \(DP[i][j]\)가 최적이 되는 가장 작은 \(k\)
\(K[i][j - 1]\leq K[i][j]\leq K[i + 1][j]\)
#include <bits/stdc++.h>
using namespace std;
int v[5003], s[5003], chk[5003][5003];
long long dp[5003][5003];
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> v[i];
s[i + 1] = s[i] + v[i];
dp[i][i + 1] = 0LL;
chk[i][i + 1] = i;
}
for (int k = 2; k <= n; k++) {
for (int i = 0; i + k <= n; i++) {
dp[i][i + k] = (long long)2e18;
for (int j = chk[i][i + k - 1]; j <= chk[i + 1][i + k]; j++) {
if (j <= i) continue;
if (j >= i + k) break;
if (dp[i][i + k] > dp[i][j] + dp[j][i + k] + s[i + k] - s[i]) {
dp[i][i + k] = dp[i][j] + dp[j][i + k] + s[i + k] - s[i];
chk[i][i + k] = j;
}
}
}
}
cout << dp[0][n] << '\n';
}
return 0;
}\(O(K\log K)\)
BOJ에 '파일 합치기 4'로 추가될 예정이다
UPDATE: BOJ에 추가되었다.
앞서 언급했듯이 이 문제는 optimal binary search tree problem의 특수한 경우인데, 이렇게 특수한 경우이기 때문에 사용할 수 있는 더 빠른 알고리즘이 있다. 이는 Garsia-Wachs algorithm으로, 정확히 이런 문제를 \(O(K\log K)\)에 풀 수 있는 알고리즘이다.
Garsia-Wachs 알고리즘에 대해 더 이야기하기 전에 한 가지 간단히 언급하고 넘어가려 한다. 알고리즘을 조금 깊게 공부했거나 정보이론 등을 공부해본 독자라면 Huffman coding에 대해 알고 있을 것으로 생각한다. Huffman coding은 external path length를 최소화하는 이진 트리를 찾는 알고리즘이자, 정보이론적인 측면에서는 어떤 symbol set에 대해 expected codeword length를 최소화하는 prefix-free binary code를 찾는 optimal coding 알고리즘이다. 이 둘은 formulation만 약간 다를 뿐 근본적으로 같은 문제이며, 위의 파일 합치기 문제에 대응할 경우, 인접하지 않은 파일의 합치기도 허용한다면 바로 이 Huffman coding으로 문제를 해결할 수 있다. 이 문제가 BOJ 13975 - 파일 합치기 3이며, solved.ac 기준 난이도 골드 5로 평가되고 있다.
하지만 파일 합치기와 파일 합치기 2는 인접한 파일의 합치기만 허용하고 있다. 이 제한은 optimal coding 문제에서 symbol set의 code의 (alphabetical) order가 고정된다는 조건으로 해석할 수 있으며, 이러한 coding 방식을 alphabetical Huffman coding 혹은 Hu-Tucker coding이라고 부른다. 따라서 파일 합치기 3이 Huffman coding을 구하는 문제라면, 파일 합치기와 파일 합치기 2는 사실 Hu-Tucker coding을 구하는 문제인 것이다. Garsia-Wachs algorithm이 바로 이 Hu-Tucker coding을 \(O(K\log K)\)에 구하는 알고리즘이다. (Hu와 Tucker의 알고리즘을 단순화한 버전이라고 한다.)
파일 크기의 배열을 \(A\), 배열의 크기를 \(n\)이라고 할 때, 이 알고리즘은 다음과 같이 동작한다.
0. 정답을 출력할 변수 \(X=0\)를 잡는다.
1. \(A_i\leq A_{i+2}\)를 만족하는 가장 작은 \(i\)를 찾는다. 그러한 \(i\)가 없으면 \(i=n-1\)이다.
2. \(A_i\)와 \(A_{i+1}\)을 합치고 이 수를 \(B\)라고 하자. \(A_i\)와 \(A_{i+1}\)은 배열에서 제거하고 그 자리에 \(B\)를 놓는다. 배열의 크기가 1 감소했고, 따라서 \(n\)은 1 줄어든다. \(X\)에 \(B\)를 더한다.
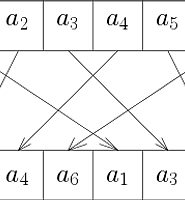
3. \(B\)의 왼쪽에 있는 수가 \(B\)보다 크거나 같을 때까지, 또는 \(B\)가 배열의 첫 번째 원소가 될 때까지, \(B\)를 왼쪽 수와 swap한다. (Bubble sort의 느낌)
4. 배열에 원소가 2개 이상 남아있으면 1번으로 돌아간다.
5. 문제의 정답은 \(X\)이다.

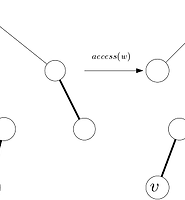
주의할 점은, 2번 단계에서 합치는 두 파일을, 실제 문제의 규정대로라면 합칠 수 없을 수도 있다. 즉 위의 과정대로 binary tree를 구성하면 문제의 조건에 위배된다. (이에 대해서는 위 예시 그림을 참조하면 이해가 빠르다.) 하지만 위의 조건대로 파일 합치기를 수행했을 때, 각 파일이 합쳐진 횟수는 동일하면서 문제의 조건을 만족하는 binary tree가 존재한다는 것을 증명할 수 있으며, 그렇게 해서 나온 답인 \(X\)이 최적임도 역시 증명할 수 있다. (왼쪽 그림이 조건에 위배되는 binary tree, 오른쪽이 문제의 조건을 만족하도록 변형된 binary tree이다.) 하지만 증명은 난이도가 있는 편이고, 디테일이 궁금하다면 Kingston이나 Karpinski, Larmore & Rytter의 논문을 직접 읽는 것을 권장한다.
사실 위의 과정을 배열이나 리스트 기반으로 naive하게 구현하면 여전히 \(O(K^2)\)의 시간이 소요된다. 그래도 Knuth algorithm보다 상수가 훨씬 작기 때문에 실제 컴퓨터에서 동작할 때 걸리는 시간은 훨씬 짧다. 이 시간을 \(O(K\log K)\)로 단축하기 위해서는 추가적인 관찰이 필요하다.
우선 처음부터 배열 전체를 보면서 1번 과정에 해당하는 \(i\)를 찾는 대신, 배열에 원소가 \(A_1\)부터 차례차례 추가된다고 상상해 보자. 1번 과정에 해당하는 \(i\)가 발견되기 전까지는, 배열은 \(A_j > A_{j+2}\)를 만족한다. 따라서 배열의 홀수 번째 원소끼리, 짝수 번째 원소끼리 따로 모아서 배열을 두 개로 분리하게 되면, 각각의 배열의 원소들은 역순으로 정렬된 상태를 유지하게 된다. 이렇게 정렬된 상태를 유지하면서, 2번과 3번 과정을 효율적으로 수행하기 위해서는 insert, binary search, delete 연산과 \(k\)번째 원소를 찾는 연산 등을 모두 \(O(\log n)\)에 수행할 수 있는 자료구조를 찾게 되고, Splay tree가 이런 용도로는 가장 적합하다. (여기서 \(n\)은 자료구조에 있는 원소의 개수이다.)
짝수 번째 원소와 홀수 번째 원소들을 Splay tree로 관리하게 되면, 위 과정을 아래와 같이 \(O(\log K)\)에 처리할 수 있다.
1. 앞서 언급했듯이 원소를 하나씩 넣으면서 조건을 만족하는 \(i\)가 생기는지 확인하면 된다. 이것만 해서는 사실 불완전한데, 자세한건 아래 3번 참조.
2. 배열에서 원소 제거는 delete 연산으로 처리하면 된다.
3. 이 단계가 난관이자 핵심이다. \(B\)가 들어갈 위치를 찾기 위해서는, 우선 두 개의 Splay tree에 \(B\)에 대한 binary search 연산을 통해, \(B\)가 들어가야 할 위치를 찾는다. 그런데 문제는, \(B\)를 끼워넣기 위해서는 두 가지 Splay tree (odd 혹은 even) 중 하나에 insert를 해야 하는데, 그냥 찾은 위치에 그대로 insert를 하게 되면 binary search tree의 기본 전제인 원소의 정렬 상태가 깨질 수도 있다. 예를 들어 \(A_{2i}\geq B\)라면, \(B\)는 배열의 \((2i+1)\)번째 원소가 되어야 하므로 Splay tree에서 들어가야할 위치는 홀수 번째 원소들의 Splay tree에서 \(A_{2i-1}\)의 바로 다음이지만, \(A_{2i-1}\leq B\)가 될 수도 있다는 것이다. 그런데 이렇게 되면 \(A_{2i-1}\), \(A_{2i}\), \(B\) 이 세 개의 수가 바로 1번의 조건을 만족하게 된다. 따라서 이 경우 재귀적으로 1번 과정으로 돌아가서 처리하고 나면, \(B\)는 비로소 Splay tree의 정렬 상태를 깨지 않고 삽입될 수 있게 된다.
위와 같이 구현이 꽤나 복잡한 편이지만, Splay tree를 능숙하게 다룰 수 있다면 아예 못할 정도는 아니다. Splay tree를 하나만 사용하는 좀더 간단한 구현도 존재한다!
여담으로, 필자가 이 포스트를 쓴 후 BOJ에 문제를 추가했다. 검수해주신 koosaga님과 TAMREF님 감사합니다.
'Computer Science > 알고리즘' 카테고리의 다른 글
| Linear Algebra in Problem Solving (2) (2) | 2022.09.02 |
|---|---|
| Linear Algebra in Problem Solving (1) (0) | 2022.08.31 |
| Link/Cut Tree (2) (7) | 2017.08.21 |
| Fast Fourier Transform (8) | 2017.08.15 |
| Link/Cut Tree (1) (2) | 2017.08.13 |