The Story of Joon
Link/Cut Tree (1) 본문
다음 자료들을 참고했다.
* 위키피디아 링크
Link/Cut Tree를 이해하거나 구현하기 위해서는 먼저 Splay Tree에 대한 이해가 필요하다. Splay Tree에 대한 내용은 여러 곳에 잘 설명되어 있다.
Link/Cut Tree는 여러 개의 트리를 관리하는 자료구조이다. 이 자료구조의 특징은, find_root(노드가 속한 트리의 루트), link(한 트리의 루트를 다른 트리의 노드로 연결), cut(루트가 아닌 노드와 부모 사이의 연결 제거) 연산을 모두 amortized O(logN)의 복잡도에 수행이 가능하다는 것이다.
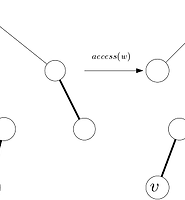
앞서 말했듯이 LCT는 여러 개의 트리로 되어있는데, 이 각각의 트리를 represented tree라고 부른다. 그런데 이 트리에는 preferred child와 preferred edge라는 특수한 구조가 있다. 노드 w가 부모 노드 v의 preferred child라는 의미는, v의 서브트리에 속한 노드 중 가장 최근에 연산이 수행된 노드가 w의 서브트리에 속해 있다는 뜻이다. 만일 가장 최근에 연산이 수행된 노드가 v 자신이거나 연산이 수행된 적이 없다면 v의 preferred child는 없게 된다. 어떤 노드와 그 노드의 preferred child를 잇는 간선을 preferred edge라고 한다.

위의 정의를 보면 알 수 있듯이, preferred child 관계는 새로운 연산이 들어올 때마다 업데이트되어야 한다. 이 그림의 두 번째 트리는 첫 번째 트리에서 노드 l에 연산이 들어왔을 때 업데이트된 모습이다. 노드 l에 연산이 들어오자 preferred edge들이 l에서 루트 노드인 a로 통하는 길을 만들어줬다는 것을 눈치챌 수 있다. 이런 식으로 연속적으로 구성된 preferred edge들을 모아서 preferred path라고 부른다. 즉 l−j−f−c−a는 하나의 preferred path다.
이제 각각의 preferred path를 새로운 트리로 관리할 것이다. 이 트리를 auxiliary tree라고 부르기로 하자. 이 트리는 key가 depth인 Splay Tree로 구현하게 된다. (편의상 depth가 작은 노드를 Splay Tree의 왼쪽에 두자) 이 auxiliary tree들끼리는 path-parent pointer라는 것으로 이어져 있다. 즉 노드 v가 노드 w의 부모 노드이고 다른 auxiliary tree에 속해있다면 두 노드를 잇는 간선을 path-parent pointer가 대신하게 된다. 이 때 주의할 점은 이 path-parent pointer는 w와 v를 잇는 것이 아니라 w가 속한 auxiliary tree의 루트에서 v로 잇는다는 것이다. 위에서 세 번째 그림은 첫 번째 트리를 auxiliary tree와 path-parent pointer들로 표현한 것이다.
이제 Splay Tree를 바탕으로 해서 연산들을 구현해 보자. 이제부터 auxiliary tree와 Splay Tree는 구분없이 쓸 것이다.
먼저 노드마다 path-parent pointer를 추가해 준다.
struct node {
node *l, *r, *p, *pp;
};이 포인터는 노드가 Splay Tree의 루트일 때만 의미를 갖는다. Rotate 함수에서 부모 노드가 루트일 경우 이 포인터 값을 넘겨받으면 된다.
void rotate(node *cur) {
node *p = cur->p;
if (cur == p->l) {
if ((p->l = cur->r)) cur->r->p = p;
cur->r = p;
} else {
if ((p->r = cur->l)) cur->l->p = p;
cur->l = p;
}
cur->p = p->p;
p->p = cur;
if (cur->p) {
if (cur->p->l == p) cur->p->l = cur;
else cur->p->r = cur;
} else {
cur->pp = p->pp;
p->pp = NULL;
}
}위에서 말했듯이 각 노드로 접근할 때마다 preferred path를 갱신해주어야 한다. 이 역할을 하는 함수 access를 만들자. 노드 v에 access(v)를 호출하면 다음 과정이 일어난다.
- Splay 연산을 통해 v가 속한 Splay Tree의 루트로 올라간다.
- v의 preferred child 관계가 있다면 모두 끊고 path-parent 관계로 바꾼다.
- v의 parent-path pointer가 NULL이라면 종료한다.
- v의 parent-path p에 Splay 연산을 행해 루트로 올린다.
- p의 오른쪽에 노드가 있다면 끊고 그 자리에 v를 연결한다. 연결이 끊긴 노드는 path-parent pointer로 p를 가리킨다.
- v에 Splay 연산을 통해 p의 자리로 올리고 3번으로 돌아간다.
void access(node *cur) {
splay(cur);
if (cur->r) {
cur->r->pp = cur;
cur->r->p = NULL;
cur->r = NULL;
}
while (cur->pp) {
node *pp = cur->pp;
splay(pp);
if (pp->r) {
pp->r->pp = pp;
pp->r->p = NULL;
}
pp->r = cur;
cur->p = pp;
cur->pp = NULL;
splay(cur);
}
}이 함수를 만들었다면 나머지 연산은 쉬워진다. 먼저 find_root(v) 함수는 access(v)를 하고 나면 preferred path로 루트까지 연결되므로 루트와 같은 Splay Tree 내에 속하게 된다. access(v) 함수가 끝나면 v는 그 Splay Tree의 루트 자리에 있으므로 왼쪽으로 계속 가면 represented tree의 루트가 나온다.
node *find_root(node *cur) {
access(cur);
while (cur->l) cur = cur->l;
access(cur);
return cur;
}cut(v) 함수는 access(v)를 한 뒤 Splay Tree 내에서 v의 왼쪽 노드와 연결을 끊으면 된다.
void cut(node *cur) {
access(cur);
if (cur->l) {
cur->l->p = NULL;
cur->l = NULL;
}
}link(v, w) 함수는 기본적으로 v가 represented tree의 루트이고 w와 다른 represented tree에 속함을 가정하고 있다. 이 함수 역시 간단한데, access(v)와 access(w)를 한 뒤 v의 왼쪽에 w를 붙이면 된다.
void link(node *root, node *cur) {
access(root);
access(cur);
root->l = cur;
cur->p = root;
}이 함수들이 어떻게 amortized O(logN)에 작동하는 지는 글머리에 첨부한 MIT 렉쳐 노트에 설명되어 있다.
Link/Cut Tree의 장점은, 여러 트리 간 연결-잘라내기가 자유롭고, Splay Tree를 기반으로 한 자료구조로 다양한 쿼리를 효율적으로 처리할 수가 있다는 점이다. 이에 관해 좀더 자세한 내용은 Link/Cut Tree (2) 참조.
연습문제
'Computer Science > 알고리즘' 카테고리의 다른 글
| Linear Algebra in Problem Solving (1) (0) | 2022.08.31 |
|---|---|
| 2015 ACM-ICPC 한국 예선 F - 파일 합치기 (2) | 2020.05.02 |
| Link/Cut Tree (2) (7) | 2017.08.21 |
| Fast Fourier Transform (8) | 2017.08.15 |
| Splay Tree (0) | 2017.08.13 |