목록Categories (13)
The Story of Joon
참고: 이 글은 필자의 기록용으로 불친절하거나 일부 선행 지식을 필요로 할 수 있습니다. 선형대수학에서 케일리 해밀턴 정리(Cayley–Hamilton theorem)는 임의의 정사각행렬 $A$에 대하여 특성다항식$$f_A(x)=\det(xI-A)$$에 행렬 $A$를 대입하면 영행렬이 나온다는 정리이다. 수학의 정석에서 케일리 해밀턴 정리를 본 적 있는 독자라면 2x2 행렬에서 아래와 같은 식으로 기억하고 있을 것이다.$$A^2-(a+d)A+(ad-bc)I=O$$이 식은 사실 2x2 행렬의 특성다항식에 $A$를 대입한 꼴로, 임의의 $n\times n$ 정사각행렬에서도 이 결과가 성립한다. 심지어 행렬의 성분이 임의의 체 $F$의 원소일 때도 성립한다. 간단해 보이는 정리이지만 증명은 생각보다 간단하지 ..
 Linear Algebra in Problem Solving (3)
Linear Algebra in Problem Solving (3)
Linear Algebra in Problem Solving (1) Linear Algebra in Problem Solving (2) Linear Algebra in Problem Solving (3) (현 포스트) 기존 두 포스트에서는 선형대수학에 등장하는 기본적인 행렬 연산과 행렬에 관련된 중요한 식을 어떻게 효율적으로 계산하는지에 대해 알아보았다. 하지만 PS에서 대놓고 이런 값을 구하라고 요구하는 문제는 드물고, 보통 선형대수학을 응용해야 하는 문제가 나오게 된다. 대표적인 예시가 1편에서 나왔듯이 XOR을 \(\mathbb{F}_2\)에서 벡터의 덧셈으로 생각하는 방식이다. 이 포스트에서는 좀더 고급 응용인, 조합론에서 선형대수학이 응용되는 예시를 다룬다. 이분 그래프의 인접 행렬 PS는 물론..
에라토스테네스의 체는 소수를 구할 때 흔히 쓰는 방식이다. 구현도 쉽기 때문에 정수론과 관련된 PS 문제에서 자주 만날 수 있다. 일반적으로는 아래와 같이 구현한다. vector sieve_of_eratosthenes(int n) { vector sieve(n + 1); vector prime; for (int k = 2; k
 Linear Algebra in Problem Solving (2)
Linear Algebra in Problem Solving (2)
Linear Algebra in Problem Solving (1) Linear Algebra in Problem Solving (2) (현 포스트) Linear Algebra in Problem Solving (3) 이 포스트에서는 선형대수학 시리즈의 전편에 이어 좀더 고급 알고리즘에 대해 다룬다. 전편에서 만든 코드베이스를 그대로 사용할 예정이므로 전편을 먼저 읽는 것을 권장한다. 특성다항식 \(n\times n\) 행렬 \(A\)의 특성다항식(characteristic polynomial) \(f_A\)는 아래와 같이 정의된다. \[f_A(x):=\det(xI-A)\] 이 다항식은 최고차항의 계수가 1인 \(n\)차 다항식이며, 아래와 같이 여러 성질을 가지고 있는 중요한 다항식이다. \(f_A(x..
 Linear Algebra in Problem Solving (1)
Linear Algebra in Problem Solving (1)
Linear Algebra in Problem Solving (1) (현 포스트) Linear Algebra in Problem Solving (2) Linear Algebra in Problem Solving (3) 선형대수학(linear algebra)은 벡터 공간(vector space)과 선형 변환(linear transformation)에 대해서 다루는 학문으로, 여러 분야에서 많은 응용이 되고 있고 수학에서의 중요성 또한 매우 높다. 컴퓨터 과학도 예외는 아닌데, 이런 이유로 많은 학교에서 컴퓨터 과학/공학과에서 기초 선형대수학을 필수 과목으로 지정하기도 한다. 이 포스트 시리즈에서는 PS에서 등장하는 선형대수학 관련 문제들을 해결하기 위한 여러 가지 선형대수학 알고리즘을 다룰 예정이다. 일반..
 사원수와 3차원 회전
사원수와 3차원 회전
3차원 컴퓨터 그래픽스에서 회전(rotation)은 매우 중요한 개념이다. 대학에서 또는 독자적으로 컴퓨터 그래픽스의 원리를 공부한 적이 있는 독자라면 3차원 회전을 사원수(quaternion)로 표현하는 방식에 대해 본 적이 있을 것이다. 단위 벡터(unit vector) \((x, y, z)\)를 회전축으로 반시계 방향으로 \(\theta\)만큼 회전시키는 동작을 사원수 방식으로는 아래와 같이 나타낸다: \[\cos(\theta/2)+x\sin(\theta/2)\mathbf{i}+y\sin(\theta/2)\mathbf{j}+z\sin(\theta/2)\mathbf{k}\,.\] 사원수는 우리가 익히 아는 일반적인 실수나 복소수와는 또 다른 시스템이다. 놀랍게도, 이렇게 나타내면 마법과 같이 3차원 ..
 2015 ACM-ICPC 한국 예선 F - 파일 합치기
2015 ACM-ICPC 한국 예선 F - 파일 합치기
BOJ 11066 - 파일 합치기 11066번: 파일 합치기 문제 소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을 www.acmicpc.net 이 문제는 2015년 ACM-ICPC 예선에 나왔던 문제로, DP 테이블을 정의하면 \(O(K^3)\)의 시간복잡도로 어렵지 않게 풀리는 문제다. 난이도는 solv..
 Link/Cut Tree (2)
Link/Cut Tree (2)
Link/Cut Tree (1) 앞선 포스트에서 LCT에 대한 기본적인 내용을 다루었는데, 이번 포스트에서는 LCT가 어떻게 활용될 수 있는지 간단하게만 알아보려고 한다. 보충 자료 같은 느낌의 포스트이다. 1. Link 연산의 확장 원래의 Link 연산은 붙이는 쪽이 represented tree의 루트인 경우에만 가능했다. 그러나 실제로 루트가 아닌 노드를 붙이고 싶을 때도 있을 것이다. 이를 위해서는 represented tree의 루트를 변경하는 작업이 필요하다. 어떤 represented tree의 한 노드를 $v$라고 했을 때, access($v$)를 하면 v에서 루트로 연결되는 preferred path가 생긴다는 점은 이전 포스트에서 알아보았다. 그런데 여기서 주목할 점은 이 preferr..
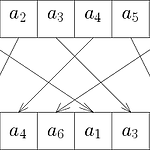 Fast Fourier Transform
Fast Fourier Transform
고속 푸리에 변환(Fast Fourier Transform, FFT)은 convolution을 $O(N\log N)$에 구할 때 활용된다. 이 포스트에서는 코드 자체보다도 FFT 알고리즘의 원리를 알아보는 것이 목적이다. 코드만 보고싶다면 맨 아래로 내려가면 된다. 푸리에 변환은 수학에서 매우 중요한 개념이며 공학 분야에서도 중요하게 다루어진다. 일반적으로 푸리에 변환은 함수를 함수로 보내는 변환인데, PS에서 활용되는 푸리에 변환은 수열을 수열로 보내는 이산 푸리에 변환(Discrete Fourier Transform, DFT)이다. 주기가 $N$인 수열 $\lbrace a_j\rbrace_{j=0}^{N-1}$의 DFT $\lbrace A_n\rbrace_{n=0}^{N-1}$은 다음과 같이 정의된다..
 Link/Cut Tree (1)
Link/Cut Tree (1)
Link/Cut Tree (2) 다음 자료들을 참고했다. * 위키피디아 링크 * MIT Lecture Note Link/Cut Tree를 이해하거나 구현하기 위해서는 먼저 Splay Tree에 대한 이해가 필요하다. Splay Tree에 대한 내용은 여러 곳에 잘 설명되어 있다. Link/Cut Tree는 여러 개의 트리를 관리하는 자료구조이다. 이 자료구조의 특징은, find_root(노드가 속한 트리의 루트), link(한 트리의 루트를 다른 트리의 노드로 연결), cut(루트가 아닌 노드와 부모 사이의 연결 제거) 연산을 모두 amortized $O(\log N)$의 복잡도에 수행이 가능하다는 것이다. 앞서 말했듯이 LCT는 여러 개의 트리로 되어있는데, 이 각각의 트리를 represented tr..
